Table des matières
Introduction
Vous êtes face à un triangle isocèle et vous devez trouver l’angle au sommet ? Pas de panique ! Même si la géométrie peut parfois sembler intimidante, il existe une méthode ultra simple en seulement 2 étapes pour résoudre cet exercice. Que vous soyez élève, parent ou simplement curieux de mathématiques, ce guide clair et rapide vous permettra de maîtriser cette compétence sans difficulté. Non seulement vous apprendrez à calculer l’angle au sommet, mais vous comprendrez également les bases essentielles des triangles isocèles. Alors, prêt à plonger dans ce monde fascinant des angles et des formes symétriques ? Allons-y !
Qu’est-ce qu’un triangle isocèle ?
Un triangle isocèle est un triangle qui possède deux côtés de même longueur. Cette caractéristique entraîne une propriété clé : les deux angles à la base, situés de part et d’autre du côté différent (la base), sont égaux. L’angle au sommet, quant à lui, est formé entre les deux côtés égaux et se distingue des angles de base.
Caractéristiques clés :
- Deux côtés égaux : Par exemple, dans un triangle ABC, si AB = AC, alors AB et AC sont les côtés isocèles.
- Deux angles de base égaux : Les angles en B et C (∠B et ∠C) sont identiques.
- Un sommet unique : L’angle au sommet (∠A) est celui formé au point de rencontre des deux côtés égaux.
- Symétrie : Le triangle est symétrique par rapport à une droite passant par le sommet et perpendiculaire à la base.
Illustration simple :
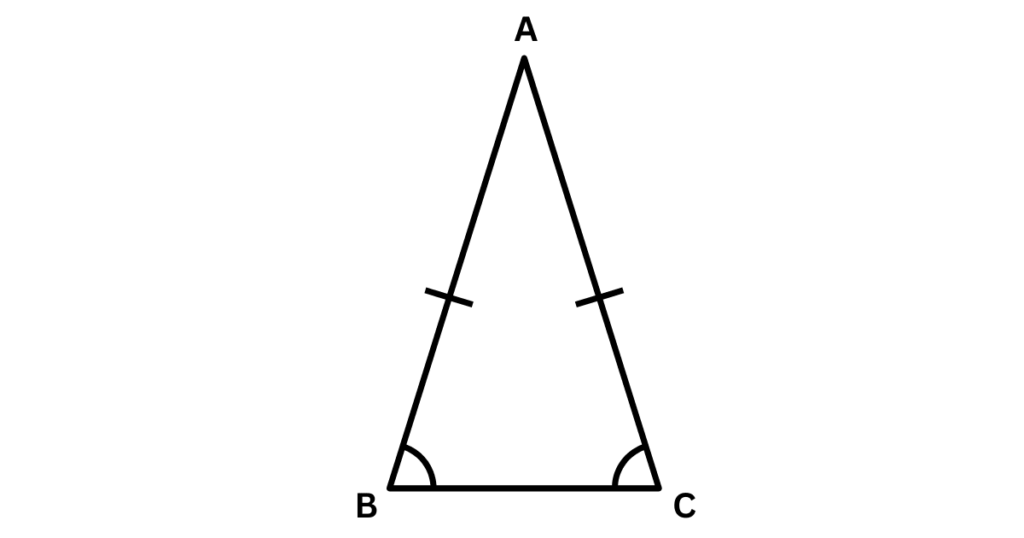
- AB = AC (côtés égaux)
- ∠B = ∠C (angles de base égaux)
- ∠A (angle au sommet)
Applications pratiques :
Les triangles isocèles apparaissent dans des domaines comme l’architecture (toits symétriques), le design (motifs équilibrés) ou encore les constructions géométriques. Leur symétrie les rend à la fois esthétiques et fonctionnels.
Pourquoi est-il important de connaître l’angle au sommet ?
Savoir calculer l’angle au sommet d’un triangle isocèle ne se limite pas aux devoirs de mathématiques. Cette compétence a des applications concrètes :
- Résolution de problèmes scolaires : C’est une base essentielle pour progresser en géométrie.
- Ingénierie et architecture : Les angles précis garantissent la stabilité des structures, comme les ponts ou les bâtiments.
- Modélisation : Dans les sciences ou les arts, comprendre les angles aide à concevoir des formes harmonieuses.
Trouver l’angle au sommet en 2 étapes
Voici une méthode simple et efficace pour déterminer l’angle au sommet d’un triangle isocèle. Elle repose sur une règle universelle : la somme des angles intérieurs d’un triangle est toujours de 180°.
Étape 1 : Calculer l’angle à la base
Dans un triangle isocèle, les deux angles de base sont égaux. Si vous connaissez l’angle au sommet, vous pouvez trouver les angles de base avec cette formule :
\text{Angle à la base} = \frac{180^\circ - \text{Angle au sommet}}{2}Exemple :
Supposons que l’angle au sommet soit de 40°.
- Calcul :
180^\circ - 40^\circ = 140^\circ
Puis,
\frac{140^\circ}{2} = 70^\circ - Résultat : Chaque angle de base mesure 70°.
Étape 2 : Appliquer la formule pour trouver l’angle au sommet
Inversement, si vous connaissez les angles de base, vous pouvez calculer l’angle au sommet avec cette formule :
\text{Angle au sommet} = 180^\circ - 2 \times \text{Angle à la base}Exemple pratique :
Supposons que chaque angle de base soit de 40°.
- Calcul :
2 \times 40^\circ = 80^\circ
Puis,
180^\circ - 80^\circ = 100^\circ - Résultat : L’angle au sommet est de 100°.
Astuces pour vérifier votre résultat
Pour être sûr de vos calculs, voici quelques astuces :
- Vérifiez la somme des angles : Additionnez l’angle au sommet et les deux angles de base. Le total doit être 180°.
- Exemple : 100^\circ + 40^\circ + 40^\circ = 180^\circ → Correct !
- Utilisez un rapporteur : Si vous avez un dessin, mesurez les angles pour confirmer.
- Analysez la logique : Dans un triangle isocèle, si l’angle au sommet est petit (par exemple 20°), les angles de base seront grands (80° chacun). Cela aide à repérer des erreurs.
Mémo : Récapitulatif rapide
| Élément | Formule |
|---|---|
| Somme des angles | 180° |
| Angle de base | \frac{180^\circ - \text{Angle au sommet}}{2} |
| Angle au sommet | 180^\circ - 2 \times \text{Angle à la base} |
Conseil : Notez vos calculs étape par étape pour éviter les erreurs.
Petit quiz interactif !
Testez vos connaissances avec cette question :
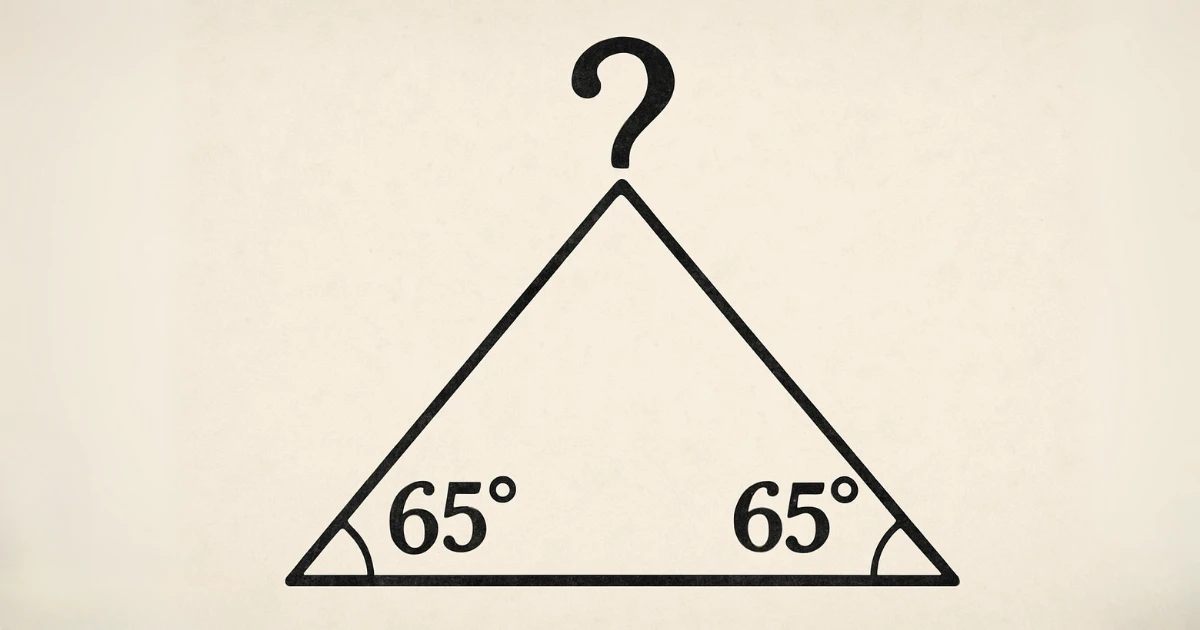
Question : Dans un triangle isocèle, chaque angle de base mesure 65°. Quel est l’angle au sommet ?
- A) 50°
- B) 60°
- C) 70°
- D) 90°
Réponse :
- Calcul : 180^\circ - 2 \times 65^\circ = 180^\circ - 130^\circ = 50^\circ
- Bonne réponse : A) 50°
Foire aux questions (FAQ)
Comment reconnaître un triangle isocèle ?
Un triangle isocèle a deux côtés égaux et deux angles de base égaux. Visuellement, il est symétrique par rapport à une droite passant par le sommet.
Est-ce que tous les triangles isocèles ont un angle droit ?
Non, seuls les triangles isocèles rectangles ont un angle de 90° (souvent au sommet ou à la base). Les autres peuvent avoir des angles variés.
Peut-on utiliser un rapporteur pour trouver l’angle au sommet ?
Oui, sur un dessin, un rapporteur est utile. Cependant, les formules sont plus précises, surtout si le dessin n’est pas à l’échelle.
Que faire si aucun angle n’est donné dans l’énoncé ?
Si vous avez les longueurs des côtés, utilisez le théorème des cosinus ou d’autres outils géométriques pour déduire les angles.
Résumé des points clés
- Définition : Un triangle isocèle a deux côtés égaux et deux angles de base égaux.
- Somme des angles : Toujours 180° dans un triangle.
- Formule pour l’angle au sommet : 180^\circ - 2 \times \text{Angle à la base}.
- Formule pour les angles de base : \frac{180^\circ - \text{Angle au sommet}}{2}.
- Propriétés supplémentaires :
- La hauteur depuis le sommet est aussi la médiane, la bissectrice et l’axe de symétrie.
- Aire : \frac{1}{2} \times \text{base} \times \text{hauteur}.
- Vérification : Assurez-vous que la somme des trois angles égale 180°.
Conclusion
Trouver l’angle au sommet d’un triangle isocèle est à votre portée grâce à ces 2 étapes simples ! La clé ? Comprendre que la somme des angles fait 180° et exploiter la symétrie du triangle isocèle. Avec un peu de pratique, vous résoudrez ces problèmes sans effort. Dessinez vos triangles, appliquez les formules et vérifiez vos résultats : la géométrie n’aura plus de secrets pour vous !