Table des matières
Introduction
As-tu déjà observé un triangle en te demandant pourquoi la somme de ses angles intérieurs est toujours égale à 180° ? Ce n’est pas juste une règle apprise par cœur à l’école : il existe une explication simple, évidente et surtout visuelle ! Comprendre cette propriété est essentiel, non seulement pour briller en mathématiques, mais aussi pour mieux saisir le monde qui nous entoure. Les triangles sont partout : dans l’architecture, la nature, l’art… Dans cet article, nous allons explorer ensemble, étape par étape, comment cette propriété fondamentale prend tout son sens. Prépare-toi à voir les triangles sous un nouveau jour et à épater ton entourage avec cette connaissance !
La somme des angles d’un triangle : rappel de la propriété
Avant de plonger dans la démonstration, rappelons cette règle incontournable :
- Dans tout triangle, qu’il soit équilatéral, isocèle ou scalène, la somme des trois angles intérieurs est toujours égale à 180° dans un espace euclidien, c’est-à-dire un espace plat.
Cette propriété est une pierre angulaire de la géométrie et sert de base à de nombreux calculs, comme la détermination des longueurs des côtés ou des hauteurs d’un triangle.
Quelques exemples
| Type de triangle | Valeurs typiques des angles |
|---|---|
| Équilatéral | 60°, 60°, 60° |
| Isocèle | 70°, 70°, 40° |
| Scalène | 50°, 60°, 70° |
Quel que soit le type de triangle, cette règle reste universelle dans un espace plat.
Démonstration visuelle de la somme des angles d’un triangle
Pour comprendre cette propriété de manière intuitive, rien ne vaut une expérience simple et concrète !
Matériel nécessaire
- Une feuille de papier épais avec un triangle dessiné
- Des ciseaux
- Un crayon ou un marqueur
- Une pincée de curiosité !
Étapes de la démonstration
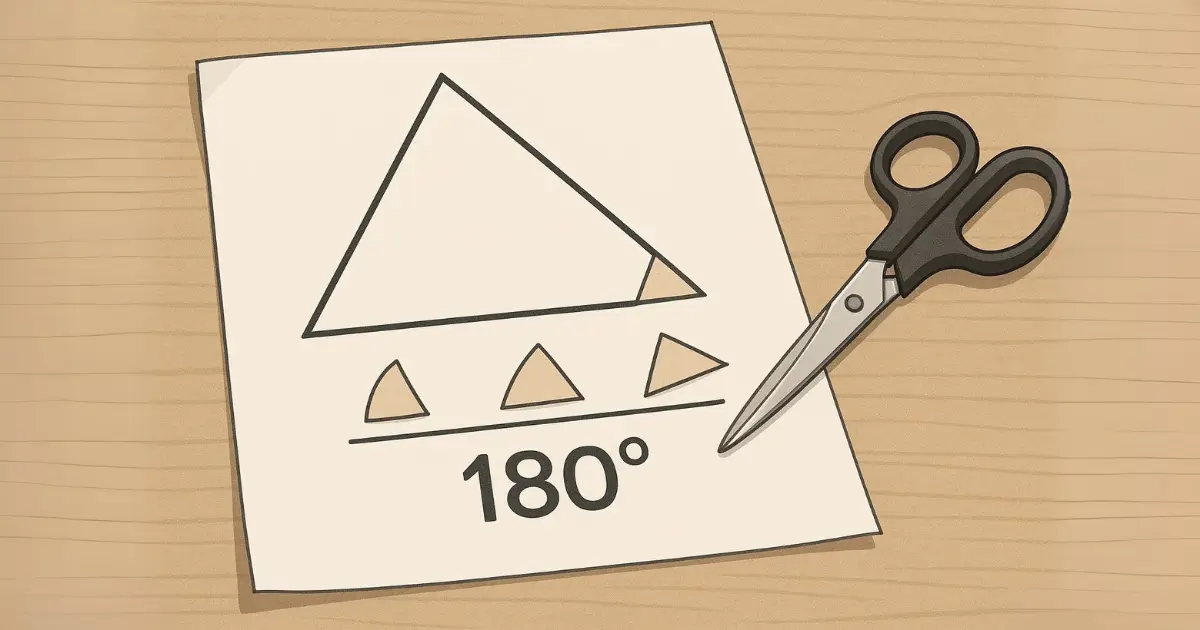
1) Dessine un triangle quelconque sur ta feuille (peu importe sa forme).

2) Découpe soigneusement le triangle en suivant ses contours.

3) Marque les trois angles avec des couleurs différentes pour les repérer facilement.

4) Découpe chaque angle avec précision.

5) Assemble les trois angles côte à côte sur une droite : place-les de manière à ce que leurs sommets se touchent et que leurs côtés soient adjacents. Tu verras qu’ils forment un angle plat, soit 180° !

Cette expérience visuelle est non seulement amusante, mais elle ancre la propriété dans ta mémoire.
Pourquoi cela fonctionne-t-il ?
- Un angle plat mesure toujours 180°.
- En plaçant les trois angles du triangle bout à bout, ils s’alignent parfaitement pour former cet angle plat.
- Conclusion : quelle que soit la forme du triangle, la somme de ses angles intérieurs est toujours 180°.
Explication géométrique simple
Pour ceux qui préfèrent une approche plus théorique, voici une démonstration géométrique basée sur les parallèles.
- Trace une droite parallèle à la base du triangle, passant par le sommet opposé.
- Les angles formés entre cette droite parallèle et les côtés du triangle sont des angles alternes-internes.
- Ces angles alternes-internes sont égaux aux angles à la base du triangle.
- En réunissant les trois angles (le sommet et les deux alternes-internes) le long de cette droite, ils s’alignent pour former un angle plat de 180°.
Voici une illustration simplifiée :
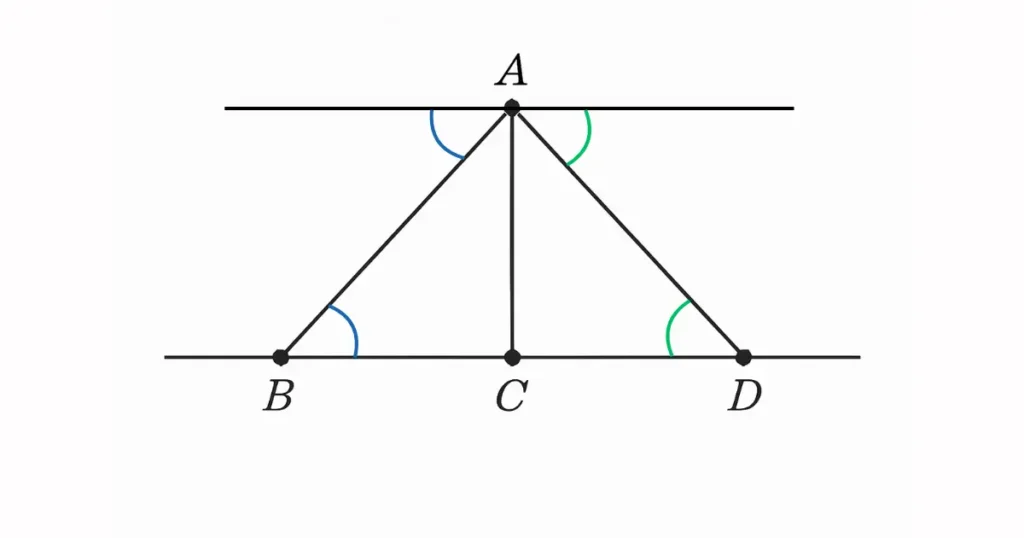
Dans cette figure :
- L’angle en A plus les angles alternes-internes (égaux aux angles en B et C) forment un angle plat.
Cette méthode montre comment la géométrie confirme cette propriété de manière rigoureuse.
Applications pratiques de cette propriété
La somme des angles d’un triangle n’est pas qu’un concept théorique : elle a des applications concrètes dans de nombreux domaines !
- Architecture : Les triangles assurent la stabilité des charpentes ou des ponts grâce à leur rigidité.
- Ingénierie : Les ingénieurs utilisent cette propriété pour concevoir des structures comme la Tour Eiffel ou des pylônes électriques.
- Jeux vidéo : Les triangles servent à créer des maillages 3D pour modéliser des objets et des paysages.
- Navigation : La triangulation, basée sur les angles, permet de calculer des positions (par exemple, en navigation maritime ou aérienne).
Exemples concrets
- Ponts : Les ingénieurs intègrent des triangles dans les treillis pour garantir la solidité.
- Graphismes 3D : Les triangles sont les unités de base pour rendre les surfaces dans les jeux vidéo.
- Navigation : Les marins déterminent leur position en mesurant les angles entre des points de repère.
Quiz interactif : Teste tes connaissances !
Question 1
Si deux angles d’un triangle mesurent 45° et 75°, combien mesure le troisième angle ?
- A) 45°
- B) 60°
- C) 90°
- D) 100°
Question 2
Dans un triangle équilatéral, combien mesure chacun des angles ?
- A) 45°
- B) 60°
- C) 90°
- D) 120°
Question 3
Si un triangle a un angle de 90°, quel est son type ?
- A) Équilatéral
- B) Isocèle
- C) Scalène
- D) Rectangle
Réponses au Quiz
Question 1 :
Réponse : B) 60°
Explication : Dans tout triangle, la somme des angles intérieurs est toujours égale à 180°. Pour trouver le troisième angle, on soustrait la somme des deux angles connus de 180° :
- Calcul : 180° – (45° + 75°) = 180° – 120° = 60°.
Question 2 :
Réponse : B) 60°
Explication : Un triangle équilatéral a trois côtés égaux et donc trois angles égaux. La somme des angles d’un triangle étant 180°, on divise cette somme par le nombre d’angles (3) :
- Calcul : 180° ÷ 3 = 60°.
Chaque angle d’un triangle équilatéral mesure donc 60°.
Question 3 :
Réponse : D) Rectangle
Explication : Un triangle qui possède un angle de 90° est appelé triangle rectangle, car il contient un angle droit. Les autres types (équilatéral, isocèle, scalène) ne nécessitent pas spécifiquement un angle de 90°, mais un triangle rectangle est défini par cette propriété.
FAQ sur la somme des angles d’un triangle
Pourquoi la somme des angles d’un triangle est-elle toujours 180° ?
Dans la géométrie euclidienne (plane), la somme des angles d’un polygone est donnée par la formule (n – 2) × 180°, où n est le nombre de côtés. Pour un triangle (3 côtés), cela donne (3 – 2) × 180° = 180°.
Cela change-t-il sur une sphère ou une surface courbe ?
Oui ! Dans la géométrie sphérique, la somme des angles d’un triangle dépasse 180°. Par exemple, sur une sphère comme la Terre, un triangle peut avoir une somme atteignant jusqu’à 540° selon sa taille.
Peut-on démontrer cette propriété autrement ?
Oui, avec la trigonométrie ou les propriétés des angles opposés. Ces méthodes plus avancées confirment toujours le résultat.
Comment démontrer avec la trigonométrie ?
Dans un triangle ABC, la loi des sinus dit : a / sin(A) = b / sin(B) = c / sin(C). En combinant cette relation avec la loi des cosinus ou d’autres identités, on peut montrer que A + B + C = 180°. C’est une approche plus formelle, mais tout aussi valide.
Résumé des points clés
- Propriété fondamentale : La somme des angles d’un triangle est toujours 180° dans un espace euclidien (plat).
- Démonstration visuelle : Découpe les angles d’un triangle et assemble-les pour former un angle plat (180°).
- Démonstration géométrique : Une droite parallèle à la base montre que les angles alternes-internes et l’angle au sommet forment 180°.
- Applications pratiques : Utilisée en architecture (stabilité), ingénierie (structures), jeux vidéo (modélisation 3D) et navigation (triangulation).
Conclusion : ce qu’il faut retenir
La somme des angles d’un triangle est toujours égale à 180° dans un espace plat. Cette propriété peut être vérifiée avec une expérience visuelle (découper et assembler les angles) ou démontrée géométriquement avec des parallèles. Elle est essentielle dans des domaines variés, de la construction à la navigation. En maîtrisant ce concept, tu développes un regard affûté sur le monde géométrique qui t’entoure.
Alors, la prochaine fois que tu croiseras un triangle, amuse-toi à vérifier cette règle simple mais puissante !