Table des matières
Introduction : Ces deux notions qui embrouillent petits et grands
Vous êtes-vous déjà senti perdu entre angles complémentaires et supplémentaires ? Ne vous inquiétez pas, vous n’êtes pas seul. Que vous soyez élève de collège, parent aidant aux devoirs, enseignant ou simplement curieux de géométrie, ces deux termes peuvent prêter à confusion. La difficulté réside souvent dans leur proximité sonore, mais aussi dans leur logique mathématique. Pourtant, une fois bien expliquées, ces notions deviennent claires, intuitives et même amusantes à manipuler.
Dans cet article, nous allons démystifier ces concepts grâce à des explications simples et illustrées, des exemples concrets, des analogies du quotidien, un quiz interactif pour tester vos acquis, et des astuces mnémotechniques infaillibles pour ne plus jamais les confondre. Vous découvrirez également des applications pratiques dans divers domaines : architecture, dessin technique, design, mathématiques, et bien plus encore.
Définition des angles complémentaires
Les angles complémentaires sont deux angles dont la somme est exactement égale à 90 degrés. En d’autres termes, lorsqu’on additionne leurs mesures, on obtient un angle droit.
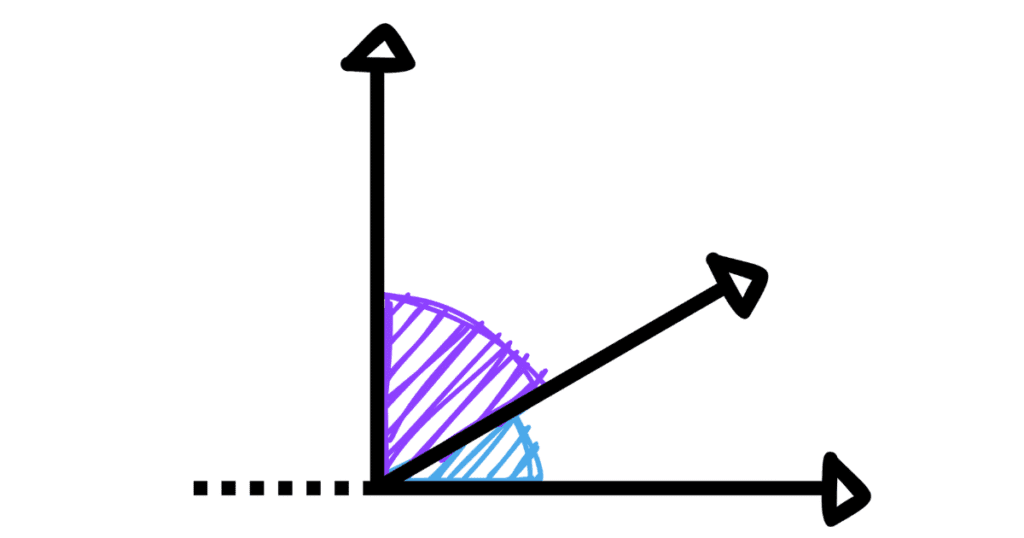
📌 Exemples :
- Si un angle mesure 30°, l’angle complémentaire mesure 60° (car 30° + 60° = 90°).
- Deux angles de 45° chacun sont aussi complémentaires.
- Un angle de 10° a pour complémentaire un angle de 80°.
Astuce mnémotechnique :
Complémentaire comme Carré = 90° (l’angle droit que forme un coin de carré parfait).
Application pratique :
- Les coins d’une feuille de papier, d’un cahier ou d’un écran forment souvent un angle droit, composé d’angles complémentaires.
- En trigonométrie, les fonctions cos(x) et sin(90° – x) sont égales, car elles exploitent la complémentarité.
- Dans le design graphique, comprendre la complémentarité permet d’agencer harmonieusement les éléments visuels.
Définition des angles supplémentaires
Les angles supplémentaires sont deux angles dont la somme est exactement égale à 180 degrés. En les additionnant, on obtient un angle plat, aussi appelé angle aligné ou angle de demi-tour.
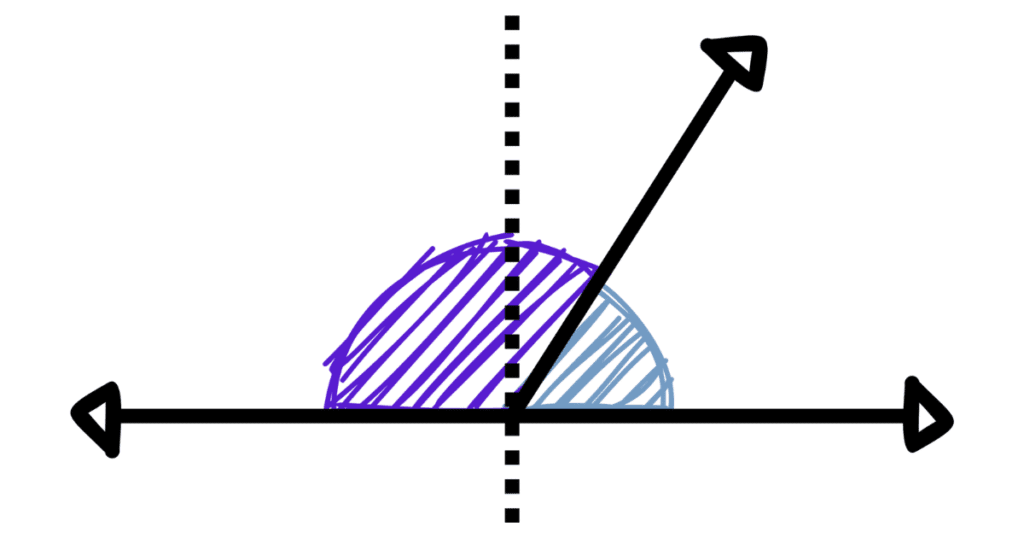
📌 Exemples :
- Un angle de 120° a pour supplémentaire un angle de 60° (120° + 60° = 180°).
- Deux angles de 90° sont également supplémentaires.
- Un angle de 135° a pour supplémentaire un angle de 45°.
Astuce mnémotechnique :
Supplémentaire comme Segment droit = 180° (ce que forme une ligne droite continue).
Application pratique :
- Lorsqu’un objet est parfaitement déplié, les deux moitiés forment souvent un angle plat.
- En architecture, les structures de ponts ou les charpentes utilisent la notion d’angles supplémentaires pour assurer la stabilité.
- Dans la navigation ou l’orientation, les angles supplémentaires permettent de calculer des caps opposés.
Tableau récapitulatif comparatif
| Type d’angle | Somme des angles | Exemples courants | Astuce mnémotechnique | Applications pratiques |
|---|---|---|---|---|
| Complémentaire | 90° | 30° + 60°, 45° + 45° | Carré (angle droit) = 90° | Trigonométrie, design, coins de page |
| Supplémentaire | 180° | 120° + 60°, 135° + 45° | Segment (ligne droite) = 180° | Construction, architecture, plans inclinés |
Comment les distinguer facilement ?
Voici 3 astuces infaillibles pour ne plus jamais les confondre :
- Associez chaque type à une forme géométrique :
- Complémentaire → Carré (coin à 90°)
- Supplémentaire → Ligne droite (alignement à 180°)
- Repérez les mots-clés et leurs racines :
- « Complémentaire » = compléter un angle droit, donc 90°.
- « Supplémentaire » = ajouter pour atteindre une ligne droite, donc 180°.
- Utilisez votre corps pour visualiser :
- Faites un L avec votre pouce et votre index → 90° = complémentaire.
- Tendez vos bras à l’horizontale → 180° = supplémentaire.
✅ Bonus : Astuce visuelle pour les élèves
Dessinez un petit carré et une ligne droite. Associez chaque mot (complémentaire/supplémentaire) à son image. Cela fixe l’association dans la mémoire visuelle.
Quiz : Testez vos connaissances !
1. Deux angles mesurent 45° chacun. Sont-ils complémentaires ou supplémentaires ?
→ Complémentaires (45° + 45° = 90°)
2. Un angle fait 120°. Quel est son angle supplémentaire ?
→ 60° (120° + 60° = 180°)
3. Peut-on avoir deux angles de 100° complémentaires ?
→ Non (100° + 100° = 200°, donc ni complémentaire ni supplémentaire)
4. Un angle de 85° et un angle de 95° sont-ils complémentaires ?
→ Non, mais ils sont supplémentaires (85° + 95° = 180°)
5. Deux angles de 90° sont-ils à la fois complémentaires et supplémentaires ?
→ Supplémentaires uniquement (90° + 90° = 180°)
FAQ – Questions fréquentes sur les angles complémentaires et supplémentaires
Quelle est la différence principale entre complémentaire et supplémentaire ?
La somme des deux angles : 90° pour les complémentaires, 180° pour les supplémentaires. C’est la règle de base à retenir.
Est-ce que deux angles obtus peuvent être complémentaires ?
Non, car un angle obtus mesure plus de 90°. Deux angles obtus dépasseraient largement les 90°, donc ne peuvent pas être complémentaires.
Les angles adjacents sont-ils toujours complémentaires ou supplémentaires ?
Pas forcément. Les angles adjacents peuvent être complémentaires ou supplémentaires si leur somme est respectivement 90° ou 180°, mais ce n’est pas une obligation.
Peut-on visualiser ces notions dans la vie courante ?
Oui ! Un coin de mur, un carnet ouvert à angle droit, ou une table rectangulaire illustrent la complémentarité. Une porte complètement ouverte ou une planche posée en ligne droite illustrent la supplémentarité.
Ces notions sont-elles utiles au-delà de l’école ?
Absolument ! Elles sont utilisées en design, en architecture, en programmation graphique, en ingénierie, et même dans certains jeux ou sports pour le calcul des angles.
✅ En résumé : ne confondez plus jamais les deux !
- Angles complémentaires = 90°
- Angles supplémentaires = 180°
- Astuces : associez-les à des formes géométriques simples (carré, ligne).
- Utilisez vos mains et objets du quotidien pour visualiser.
- Entraînez-vous avec des quiz et des dessins simples pour mémoriser durablement.
- Appliquez ces connaissances à la vie réelle et dans les matières scientifiques.
🧾 Conclusion
Comprendre la différence entre angles complémentaires et angles supplémentaires est bien plus qu’un simple exercice scolaire : c’est une clé pour naviguer aisément dans le monde de la géométrie, mais aussi dans des domaines concrets comme l’architecture, le design ou même la robotique. En maîtrisant ces deux notions fondamentales, vous gagnez en précision, en logique et en intuition spatiale.
En fin de compte, souvenez-vous : un angle droit se complète, une ligne droite se supplée. Grâce aux astuces, aux analogies et aux exercices de cet article, vous êtes désormais armé pour aborder ces concepts avec confiance et clarté. À vous de jouer maintenant — et pourquoi ne pas aider quelqu’un d’autre à les comprendre à votre tour ?